图论〔Graph Theory〕是数学的一个分支。它以图为研究对象。图论中的图是由若干给定的点及连接两点的线所构成的图形,这种图形通常用来描述某些事物之间的某种特定关系,用点代表事物,用连接两点的线表示相应两个事物间具有这种关系。
复制粘贴结束,在算法的学习过程中,图论是必学的且及其重要的知识,本章将会介绍图的基本概念(顶点与边、有向图无向图、路径、生成树等)以及图的主流存储方式(邻接矩阵、邻接表)。
注:本章专业性概念都出自于《数据结构、算法与应用》,可放心使用。
一、图的表示及基础分类
图是有限集 V 和 E 的有序对,表示为 G =( V,E ),其中 V 的元素称为顶点,E 的元素称为边。每一条边连接两个不同的顶点,用元组( i , j )来表示,其中 i 和 j 是边所连接的两个顶点。
我们可以用图示的方法来形象的表示一个图,其中圆形内是顶点,顶点和顶点之间连接的线段是边,得到下图:
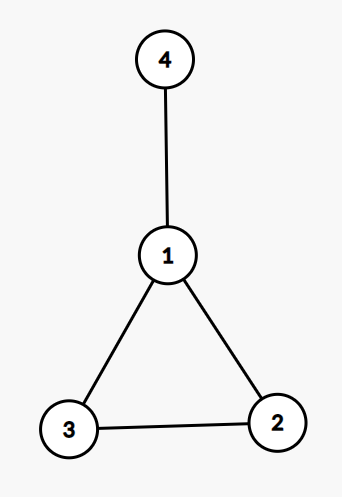
通过上图可知顶点4与顶点1有一条边进行相连,在形式上着两边的关系是互通的,而有的时候会出现单向连通的情况,比如:
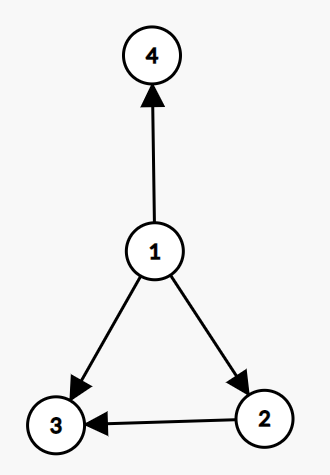
在上图中顶点1与顶点4存在的边是1指向4,代表了两个点之间的关系是单向的,也就是具有了方向性,我们将这种边称为有向边,而不具有方向性的叫做无向边。
通过边的方向性进行分类
通过边的性质,我们也可以进一步的对图分类:
1.有向图:如果图的所有边都是有向边,那么该图叫做有向图;
2.无向图:如果图的所有边都是无向边,那么改图叫做无向图;
3.混合图:在一个图中既存在有向边也存在无向边。
除了用画图的方法,我们还可以用集合法进行表示,比如针对图2,我们可以用集合 G =( V ,E ) 表示为:
通过边的连接方式进行分类:
重边:在图中出现两条完全相同的边;
自环:字面意思,在一个图中存在一条边自己连接自己,数学意义上即:∃e=(u,v)∈E,且u=v;
通过上述两个概念又可以将图分为以下两种:
简单图:不允许存在重边和自环;
多重图:允许图中存在重边和自环。
通过边的权值进行分类:
在实际的应用中,我们可能要为每条边赋予一个表示成本的值,比如抽象两个道路间的距离、抽象两地行程的时间等,而这个值我们称之为边权。因此带有边权的有向图称为加权有向图,带有边权的无向图称为加权无向图。这里将上面的图赋予边权,如下图所示:
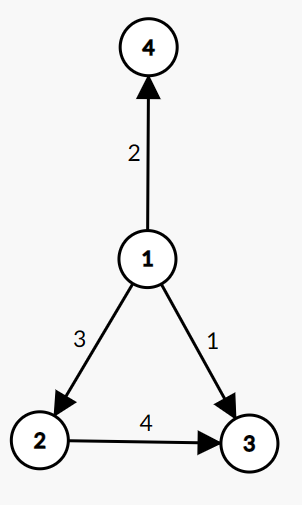
二、度、入度、出度
度:
在一个无向图中,与一个顶点 i 相关联的边数称为该顶点度(degree)di。通俗的讲就是一个点连接其他点的个数,我们还是以最初的图片为例,其中d1 = 3,d2 = 2,d3 = 2,d4 = 1。

特性:
设 G =( V , E)是一个无向图。令 n =|V|,e=|E|,则有:
1. $ \sum_{i=1}^{n}d_i=2e$
证明:
在无向图中,每一条边都与两个顶点相关联,因此所有顶点的度之和是总边数的 2 倍。
2. 0 ≤ e ≤ n·(n-1)/2
证明:
每个顶点的度都一定在 0 到 0 ~ 1之间,因此所有顶点度的和在 0 到 n·(n - 1) 之间,又通过1结论可知e在0到n·(n-1)/2之间
入度和出度:
设G是一个有向图。顶点 i 的入度(in-degree)dini是指关联至该顶点的边数。顶点 i 的出度(out-degree)douti是指关联于该顶点的边数。简单来讲入度就是被其他点连接的个数(箭头指向自己的),出度就是连接其他点的个数(剪头指向其他顶点的)。我们依然来举个例子,在下图中:din1=0,din2=1,din3=2,din4=1;dout1=3,dout2=1,dout3=0,dout4=0。

特性:
设 G =( V ,E)是一个有向图。令 n =| V |,e=| E |,则有:
1. 0 ≤ e ≤ n·(n-1)
2. din1+din2+····+dinn = dout1+dout2+····+doutn = e
因为篇幅原因就不在这里做证明了,感兴趣的可以类比无向图的版本自己推一遍或者查阅相关资料。
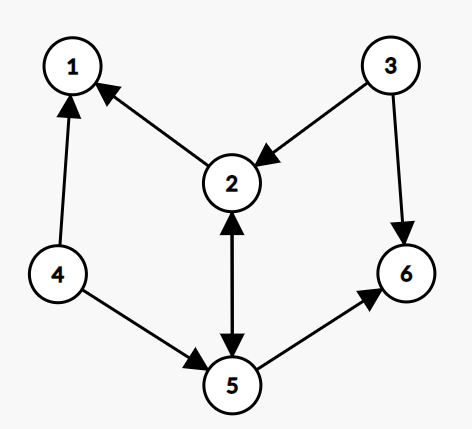
三、路径
这个概念顾名思义,专业点说就是若干个点连接起来的边的集合。一般来讲每条边是具有边权的,路径的长度则是这条路径的边权之和。在路径的长度和经过的点上又细分为以下三种情况:
1.简单路径:路径连接的点两两不同
2.回路:路径头尾相接
3.简单回路:路径仅头尾相接
路径问题在图论中非常常见,在实际中也有很大的用处,其中最典型的就是最短路径问题,在以后的文章中也会单出来讲解。
四、生成树
在讲解之前,我们先引入一些概念:
G =(V ,E)是一个无向图。 G 是连通的,那么当且仅当 G 的每一对顶点之间都有一条路径。比如下面第一张图(图1)就是连通的,因为点1、2、3、4都存在至少一条路径使其能到达任意一个点;而第二张图(图2)则不是,因为点1、2、3都无法到达点5、6、7、8。

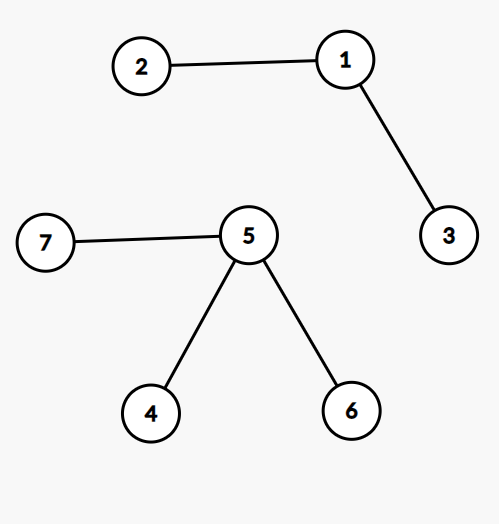
我们不难发现,在图1中虽然已经达到了连通,但一个顶点到另一个顶点可能存在多种不同的路径,进而可以发现,即使去掉一些不必要的边,图依然还是连通的,比如去掉(2,3)或(1,4),整个图依然连通。
如果H的顶点和边的集合分别是 G 的顶点和边的集合的自己,那么称图 H 是图 G 的子图(subgraph)。一条始点和终点相同的简单路径称为环路(cycle)。比如在图1中1,2,3,1就是一条环路。显然,若一个连通图中不存在环路那么这个连通无向图就是一颗树。
生成树:一个 G 的子图,如果包含 G 所有顶点,且是一棵树,则称 G 为生成树。
通俗的来讲,生成树就是去掉原连通图的一些边,使得到的新图连通且不存在环路,有了上述的概念支撑,我们就可以简单列举几种图1的生成树:

生成树的应用可以联系于实际的生产活动中,比如在道路建设中,在保证每条道路都可以互相到达的前提下减少回路的出现则可以大幅降低建设成本,而在有 n 个顶点的连通图中至少有 n - 1条边,在达到最少边时优先选择建设代价小的边则能使总代价最小,这个最小代价的生成树则称为最小生成树。最小生成树在图论中也非常重要,后续会详细带来求解的方法。
五、图的建立与存储
一切的理论最后都要进行代码的实践,在最后我们来说一下图的建立和存储,这里给大家介绍两大类(三种)存图方式:邻接矩阵、邻接表(邻接链表、邻接数组)。
邻接矩阵
邻接矩阵就是将图存在一个 n * n 的矩阵(数组)中,来达到存储图中所有邻接关系的需求。一个 n 个顶点的图 G =( V , E ),若 G 是一个无向图,那么其中的元素定义如下:
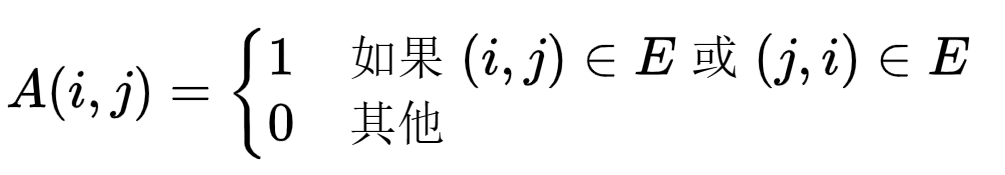
如果 G 是有向图,那么其中的元素定义如下:

通俗一点的说,如果A(i,j)的值为1,那么代表有一条i与j相连的边,在程序中我们通常用二维数组来存储矩阵,我们还是用前面的图为例来建立一个邻接矩阵:

int arr[5][5] = {
{0 0 0 0 0},
{0 0 1 1 1},
{0 1 0 1 0},
{0 1 1 0 1},
{0 1 0 1 0}
};因为数组下标从0开始的缘故,我们抛开第一行和第一列,剩下的部分就很清晰的表示了点与点之间的关系,在无向图中,因为没有方向,所以 arr[i] [j] 和 arr[j] [i] 的值一定相等,进一步可以发现整个矩阵沿(1,1)到(n,n)连成的直线对称,所以无向图的邻接矩阵是一个对称矩阵,因此我们可以利用这一特性对空间上做一些优化,但这里因为篇幅和深度的原因就不再探究了,想学的可以去查对应参考书学习。这里也给出无向图邻接矩阵创建的参考代码:
int n,m;
cin >> n >> m;
int G[n+1][n+1];
memset(G,0,sizeof G);
for(int i = 1;i<=m;i++){
int u,v;
cin >> u >> v;
G[u][v] = 1;
G[v][u] = 1;
}如果存有向图那么只需要存一次边即可,不需要存反向边,如果是存带边权的图呢?很简单,只需要将固定值1换成对应的边权即可。
优点:
1.存储方式容易理解
2.可以O(1)的时间内实现删除、修改、添加操作
缺点:
1.遍历一次需要O(n2)的时间
2.内存开销过大,空间浪费严重,当题目顶点过多时会爆空间
邻接链表
因为邻接矩阵对空间消耗过大的缘故,所以在平常的应用场景很少,我们一般都采用邻接表来存图。在网上和很多的教材内一般都用链表的形式来存储,这种方法叫邻接链表,其原理就是把每个点所连的边用链表串在一起,在使用时直接在链表中访问即可,我们还是以上面的图为例,模拟一下邻接链表的存储方式:


因为是运用了链表的思想+数组模拟链表,所以如果没有学对应的前置芝士的需要提前去学一下,如果知道以后那么存起来就非常容易了,这里给出参考代码:
#include<bits/stdc++.h>
using namespace std;
const int N = 100010, M = N * 2;
int n;
//h[i]是以i为起点的第一条边的编号
//e[i]是i这条边终点的结点编号
//ne[i]是和i这条边同起点的下一条边的编号
int h[N], e[M], ne[M], idx;
void add(int a, int b)
{
e[idx] = b;
ne[idx] = h[a];
h[a] = idx;
idx++;
}
int main()
{
scanf("%d", &n);
memset(h, -1, sizeof h);
for (int i = 0; i < n - 1; i ++ )
{
int a, b;
scanf("%d%d", &a, &b);
add(a, b), add(b, a);
}
return 0;
}这里给出的是无权无向图的存储方式,有向图则边存一次即可,如果有权则需要多一个存权值的数组。
优点:
1.省空间,几乎所有的图都可以用这种方式存,空间复杂度O(n+m);
2.遍历一次全图时间复杂度仅需O(n+m)
缺点:
实现复杂,使用数组较多,做题不注意很容易出错,且对新手不友好。
对于链式前向星,和邻接表的实现思路大同小异,所以在这里就不再讲了。
邻接数组
顾名思义,就是把前者链表的部分用数组实现出来,一般在C++中常用vector来存储,这样就防止了使用邻接链表时因为存储细节的原因导致的错误,可以说对新手极其友好,缺点是相对于邻接链表,数组的方式在效率上会稍慢一些,但基本可以忽略不计(一般的题目没有卡这个的)。因为和邻接链表的原理很相似,所以就不再画图展示空间模型(就是把指针换成了数组元素),我们直接给出存图的实现代码:
#include <bits/stdc++.h>
using namespace std;
vector<vector<int>> G;
int main() {
int n,m;
cin >> n >> m;
G.resize(n+1);
for(int i = 1;i<=m;i++){
int u,v;
cin >> u >> v;
G[u].push_back(v);
G[v].push_back(u);
}
system("pause");
return 0;
}同样是给出的无向图的存储方式,如果存有权图时可以在vector中嵌套一个pair容器,第一个元素存指向的边,第二个元素存边权,这样理解起来难度就会小很多,而且相对于邻接矩阵,空间上的开销也少了不少,个人很推荐这种存图方法,可以来试试看。
六、总结
本章主要是对图论的学习做铺垫,里面的知识算是学图论必备的,尤其是对于存图的方法,尽快选择出最适合自己的存图方式,对以后的学习会有很大的帮助,方法很多,选择最适合自己的才重要。后续我也会继续更新图论相关的文章,比如:拓扑排序、最短路、最小生成树等,可以多多关注我的动态。
好了本期内容到这里就结束了,如果你认为该文章对你有一点点帮助,也请希望收藏我的主页或者关注微信公众号:ModCx,如果有什么疑问或者建议也可在微信公众号后台留言,你们的支持就是我的动力,让我们下期再见~

When is the next update? I can’t understand Dijkstra’s algorithm at all . Plz
U website’s captcha is so cool 🙂
Ohh the ASCII art will auto trans to emoji !