今天我们要学习的是前缀和,说到前缀和它本身与其他算法不同,更像是一种优化的思想,一种数学规律,理解起来也比较简单,这篇文章主要讲解的为一维前缀和与二维前缀和的实现以及使用场景,那么现在开启我们今天的教学。
一、前缀和的引入
在讲解之前,我们先给出一个问题:
输入一个长度为 n 的整数序列。
接下来再输入 m 个询问,每个询问输入一对 l,r。
对于每个询问,输出原序列中从第 l 个数到第 r 个数的和。
示例:
输入:
5 3 2 1 3 6 4 1 2 1 3 2 4输出:
3 6 10
对于这个问题相信大家应该很快就能写出答案,我现在放一个样例代码,可以看看与各位的思路是否一样:
#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int arr[N];
int main() {
int n,m;
cin >> n >> m;
for(int i = 1;i<=n;i++){
cin >> arr[i];
}
for(int i = 1;i <= m;i++){
int q1,q2;
cin >> q1 >> q2;
int sum = 0;
for(int j = q1;j <= q2;j++){
sum += arr[j];
}
cout << sum << endl;
}
return 0;
}在第一次访问时求第1到第2个元素的和,即为2+1 = 3,求第1到第3个元素和,则为2+1+3 = 6,求第2到第4个元素和,则为1+3+6 = 10;将输入的数据存入数组中,每一次询问时遍历需要查询的区间并累加,得到最终的结果。这是最简单的一个方法,但如果当询问的次数较大的情况呢?那我们就会发现有一些数会重复的相加多次,这样下来很显然每一次遍历区间的方法就比较低效了,这个时候就可以用到我们今天要学的前缀和。
二、一维前缀和的数学引入与实现
还是以上面的题为例,我们不妨来画一个图:

在输入的数据中,我们会用数组将数据依次存起来,而我们需要要做的优化则是是否有方法可以一次性将其所有状态全部储存,来避免重复相加的情况,在后续读取任意一段区间和可以直接得到结果呢?当然是有的(狗头)!
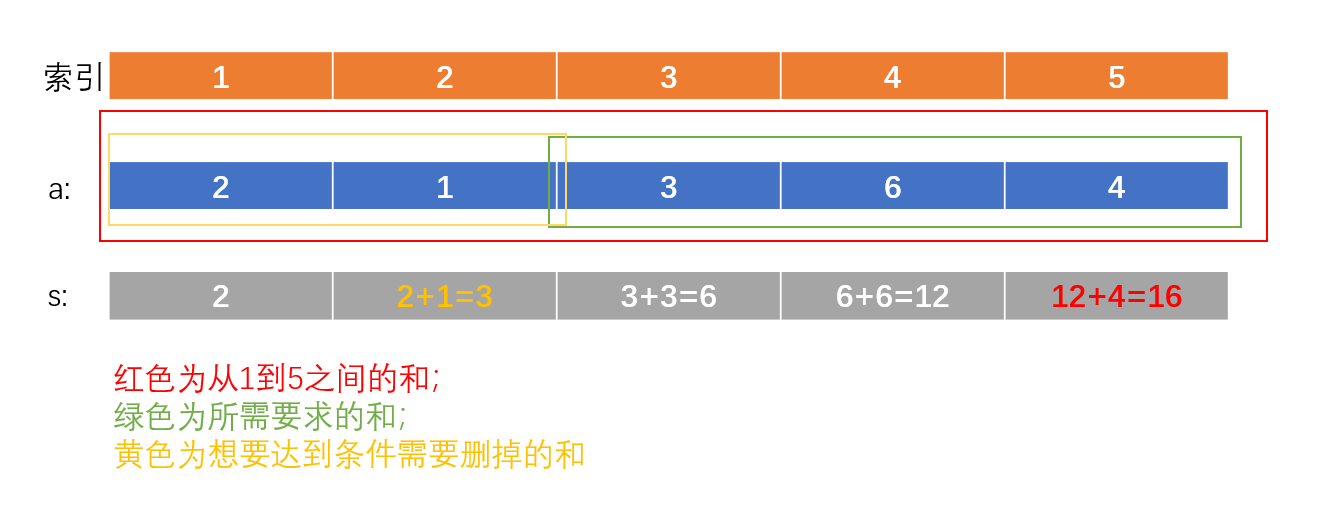
假设我们要求解的是从第一个元素到第五个元素之间的和,即整个序列的总和,那么很显然直接将五个数相加即可得到最终答案16。而我如果紧跟着说,我想得到第二个元素到第五个元素之间的和,那我们完全可以根据上一步的答案16减去第一个元素2就能得到我想要的答案14,第三个到第五,那么则是16 - (2 + 1)、第四到第五也同样的道理。
那如果我最开始需要求第一到第四个元素之间的和呢?很简单,直接2+1+3+6 = 12,而此时如果我要第二到第四个元素之间的和呢?和上面的例子一样,12 - 2 = 10,得到第三到第四个元素之间和也是同理。
看到这里是否总结出规律了呢?在[l,r]区间内,只要有存有从1到l-1之间的和以及从1到r之间的和,即可直接直接得到答案。进一步来讲,将每个元素对应的在其前面元素的总和存起来,在访问时即可实现直接访问,这个思想则被称为前缀和。
我们通过下图来详细说一下,在此时我们定义两个数组,一个为数组a,就是存储读入的元素;另一个数组为s,存储从1到元素自己本身 之间的元素和(听不懂的直接看图吧)。

那么此时我如果想访问第3个元素到第5个元素之间的和,即l = 3,r = 5,应该怎么操作呢?我们拿到第1到第5个元素之间的和,即s[5] = 16(数组默认从1开始,后面会说为什么从1开始),但我们发现这个过程中多算了第1和2个元素,需要减去,而需要减去的数通过看图就可以发现恰好为s[2],所以若得到第3到第5之间的元素和,只需要输出s[5] - s[2]即可,推广到一般形式即为:
但在推出公式的同时我们也同样要验证公式的通用性,其中最需要检测的即为边界条件,假如我需要得到的是第一个元素到第三个元素之间的和,应该怎么求?很显然通过上面的结论:ans = s[3] - s[0],但这个时候问题就来了,s[0]在上表中并没有定义,这样来算会不会出现问题?这个时候就是使用前缀和的一个小技巧了:初始时将数组全部元素赋值为0,数组的数据从下标为1开始存储,就可完美避免访问s[0]时出现的问题,因为s[0]本身为0,不会影响最后的结果。
在C++中,若将数组开到全局区则数组中全部元素将默认赋值为0,若开到函数内则每个元素会分配一个随机值,若想达到与全局区同样的效果则需要调用memset()函数或者手动更改赋值。
那么说了这么多,现在我们就用代码来实现一下一维情况的前缀和:
#include <bits/stdc++.h>
using namespace std;
const int N = 100010;
int a[N];//存放读入数据数组
int s[N];//前缀和数组
int main() {
int n,m;
int l,r;
scanf("%d %d",&n,&m);
for(int i = 1;i<=n;i++){
scanf("%d",&a[i]);
s[i] += s[i-1] + a[i];//预处理前缀和
}
for(int i = 1;i<=m;i++){
scanf("%d %d",&l,&r);
printf("%d\n",s[r] - s[l-1]);//通过前缀和公式直接访问
}
system("pause");
return 0;
}三、一维前缀和的时间复杂度分析
在学习完一维前缀和的原理与代码实现后,我们来简要分析一下一维前缀和时间复杂度,在给出的示例代码中,我们可以发现初始化前缀和数组中一共执行了n次,因此初始化过程的时间复杂度为O(n),而在访问过程中,通过直接读取数组中对应的元素来进行求解,时间复杂度为O(1),因此概括一下即为O(n)复杂度预处理,O(1)复杂度访问,而对比我们最初给到的暴力解法,效率则有明显的提升。
但在分析时间效率的同时如果我们关注到了空间,则就发现了一个点:前缀和的解法和普通暴力解法相比,空间开销大了一倍,前缀和用到了两个数组进行求解,而暴力解法则是一个数组解决问题。
这种通过增大空间的开销来将程序的时间效率提升的方法,则为以空间换时间,也是平常算法优化的一种常用思路,上一篇我们讲解的埃氏筛和欧拉筛也是用了相同的思想,都是通过增大空间开销来提高时间效率。
四、二维前缀和的递推及实现
在说完一维前缀和后,我们顺着思路来看看下一道题:
输入一个 n 行 m 列的整数矩阵,再输入 q 个询问,每个询问包含四个整数 x1,y1,x2,y2,表示一个子矩阵的左上角坐标和右下角坐标。
对于每个询问输出子矩阵中所有数的和。
输入格式
第一行包含三个整数 n,m,q。
接下来 n 行,每行包含 m 个整数,表示整数矩阵。
接下来 q 行,每行包含四个整数 x1,y1,x2,y2,表示一组询问。
输出格式
共 q 行,每行输出一个询问的结果。
输入样例
3 4 3 1 7 2 4 3 6 2 8 2 1 2 3 1 1 2 2 2 1 3 4 1 3 3 4输出样例
17 27 21
我们会发现这个题和上面的题是及其相似的,不一样的点在于上面的题数据分布在一维的线上,而这道题为一个二维矩阵,但需要求解的问题都是相同的,都是区间和,那么我们能不能类比上面的一维前缀和,来推导出二维前缀和呢?
1.二维前缀和数组的构建
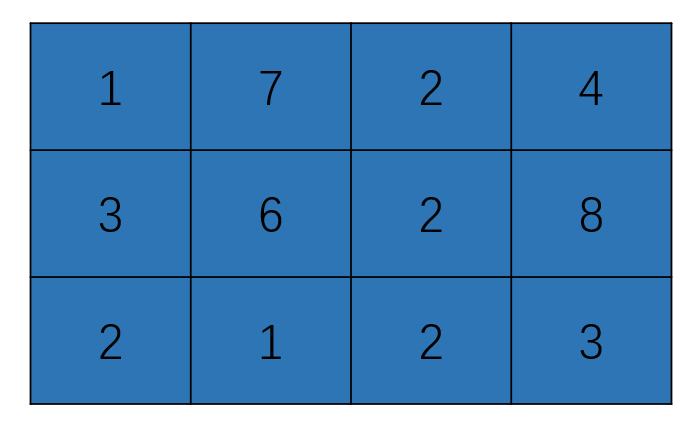
我们先将给出的数据做成二维矩阵的图像,类比我们前面的一维情况,我们这时也可以去定义一个二维的前缀和数组,在一维中,前缀和数组每一个元素代表的是在他之前包含他本身的元素和,而在二维中,每个元素所表示的意义应该是什么呢?即为围成的区域内的元素和。确定他的含义后,我们就要去寻找递推的关系,先从简单的入手,s[1] [1] = 这个毫无疑问,而s[1] [2],即第一行第二列的前缀和应该为其围成的矩阵和1 + 7 = 8,s[2] [1]即第二行第一列的前缀和应该为1 + 3 = 4。
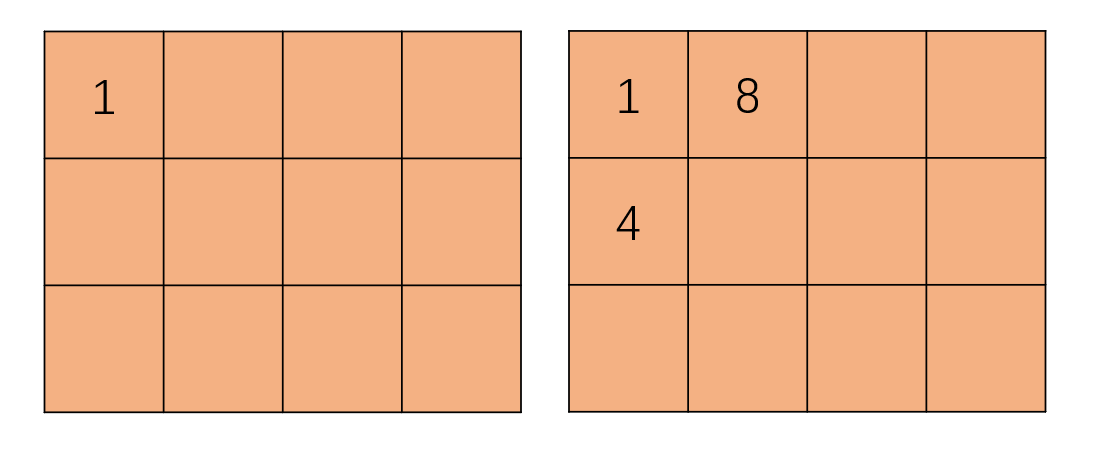
这些结论都是显而易见的,实际和一维前缀和并无太大区别,但如果再继续扩展呢?到了s[2] [2],即求出2x2的矩阵和,为1+7+3+6=11.但我们如何用前面的结果去递推出来呢?从下图我们可以发现,s[1] [2]和s[2] [1]存着行与列的前缀和,我们此时将两者相加,则能得出这L型的总和,但细心的同学会发现,在这个过程中a[1] [1]这个元素被加了两次,因此在最后需要再减去s[1] [1] (如果有不明白为什么是减s[1] [1]而不是a[1] [1]的同学,不妨试试求s[3] [3])才是L型的元素总和,最后加上新假如的元素a[2] [2],得到公式:
下面举例中出现了笔误,本身的 s[4][4]= a[2][2] + s[1][2]+s[2][1] - s[1][1] 应该变为 s[2][2]= a[2][2] + s[1][2]+s[2][1] - s[1][1]
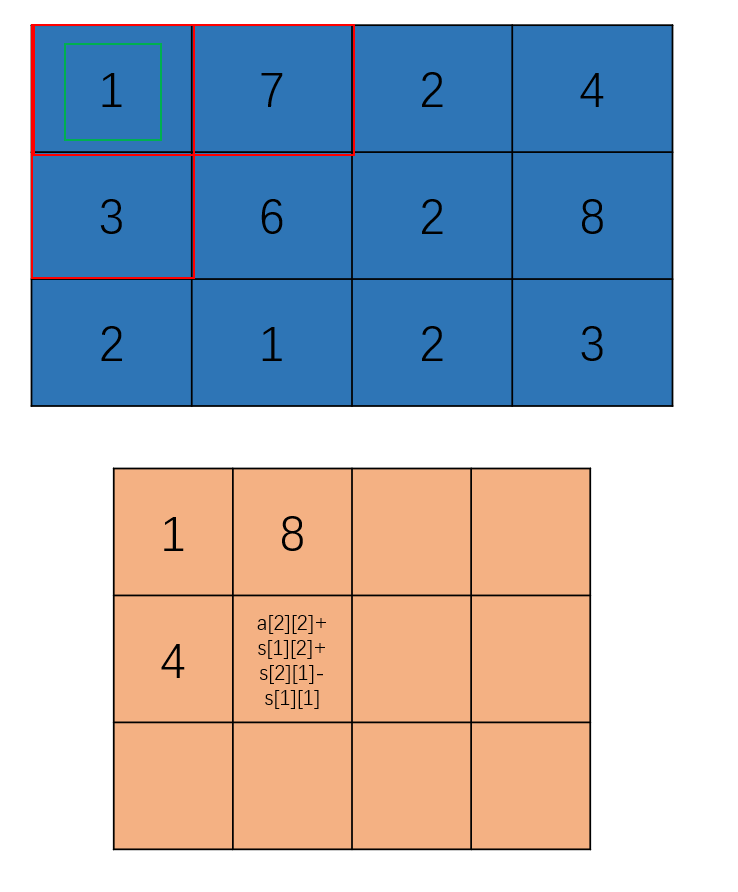
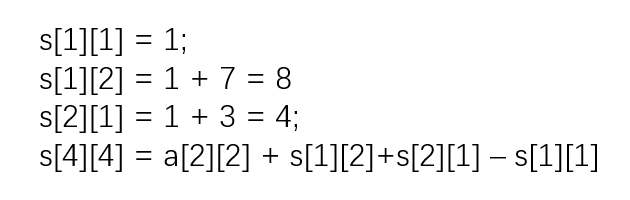
因此二维前缀和的数组就构建完成了,接下来就到我们最关键的一步:如何求任意的子矩阵和
2.求解任意子矩阵和
假如我们要求解下图中红框框起来的矩阵和,应该怎么通过二维前缀和数组来求解呢?
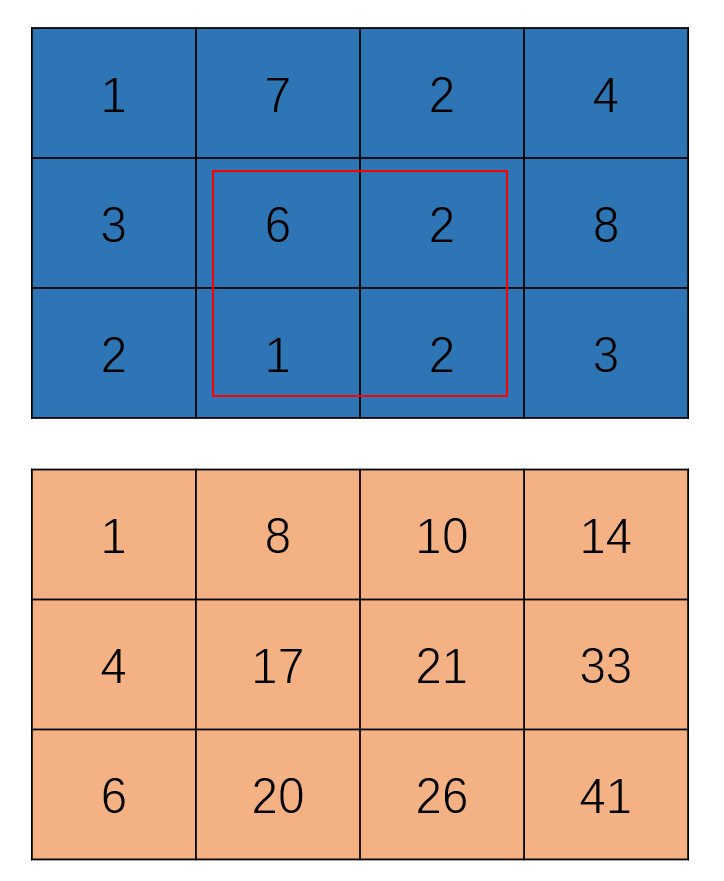
其实从一维前缀和就可以总结出一些经验,在求解时我们会先用其边界求出从(1,1)到(3,3) (此处坐标为数组意义的坐标,即第一个为行,第二个为列)的和,在通过一些方法将多余的元素减去,那么对于这个应该怎么操作呢?我们会发现,将所求矩阵的上半部分圈起来对应的为s[1] [3],左半部分圈起来对应为s[3] [1],将其与s[3] [3]作差在整体上只剩下所求部分矩阵,但与一维前缀和相同,有多减的部分,即s[1] [1],那么将其整理,得到的公式则为ans = s[3] [3] - s[3] [1] - s[1] [3] + s[1] [1]。
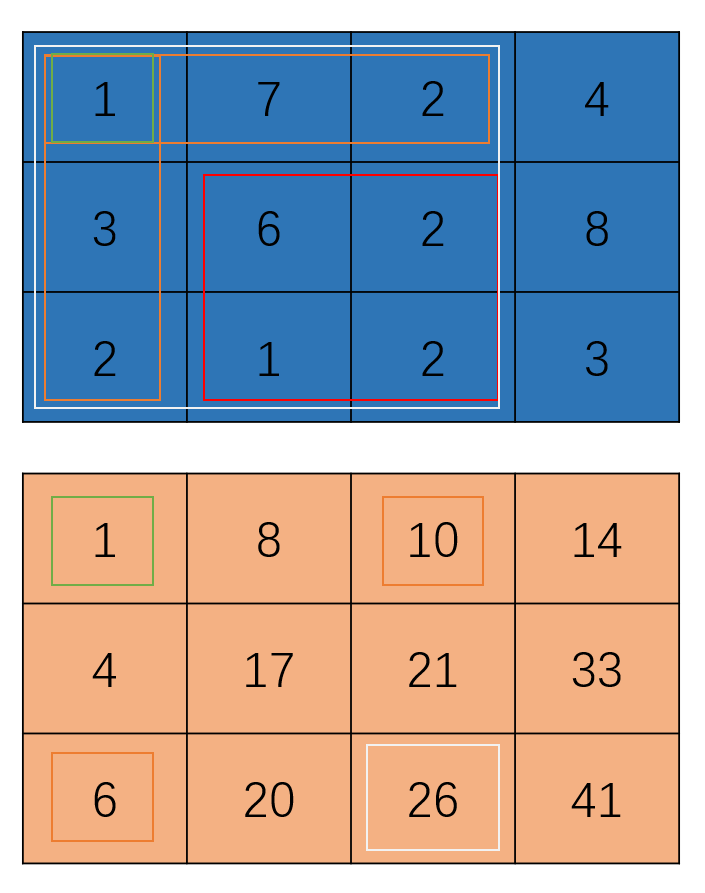
而现在将坐标换成x1,y1,x2,y2,总结一下一般规律,任意子矩阵和的公式则为:
因此,二维前缀和的公式推导完成,接下来结合前面推出的公式,来用程序具体实现一下:
#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int a[N][N];//读入数组
int s[N][N];//前缀和数组
int main(){
int m,n,q;
scanf("%d %d %d",&n,&m,&q);
for(int i = 1;i<=n;i++){
for(int j = 1;j<=m;j++){
scanf("%d",&a[i][j]);
}
}
for(int i = 1;i<=n;i++){
for(int j = 1;j<=m;j++){
s[i][j] = s[i][j-1] + s[i-1][j] -s[i-1][j-1] + a[i][j];//预处理前缀和
}
}
while(q--){
int x1,x2,y1,y2;
scanf("%d %d %d %d",&x1,&y1,&x2,&y2);
printf("%d\n",s[x2][y2] - s[x1-1][y2] - s[x2][y1-1] + s[x1-1][y1-1]);//求解任意子矩阵和
}
system("pause");
return 0;
}这样二维前缀和的实现也就此完成,我们也可以发现,相比于常规的暴力解法,二维前缀和也为程序的时间效率带来了很大提升,当然,这也是以空间为代价换来的。
五、总结
前缀和更多算是一种数学思想,对程序在数学意义上的调优,比较简单易上手,对于求解子区间和的问题是一个很好地方法,可以很好地提高运行效率。在这里也给出一些练习的题目,可以帮助大家更好的掌握前缀和的思想,为洛谷题号:P3397、P1719。
好了本期内容到这里就结束了,如果你认为该文章对你有一点点帮助,也请希望收藏我的主页或者关注微信公众号:ModCx,如果有什么疑问或者建议也可在微信公众号后台留言,你们的支持就是我的动力,让我们下期再见~
