今天我们要学习的是差分,差分与我们之前讲过的前缀和一样,更多是一种优化的思想,一种数学规律,甚至可以说前缀和与差分是一个相伴相生的关系,可以理解为“一对情侣”,因此如果对前文的前缀和的理解比较深刻的话,理解差分可能就会相对简单一些,差分也分为一维差分和二维差分,接下来我将通过情景引入、数学推导、代码实现的方式来讲解差分的原理。
一、差分的引入
我们和上期一样,先抛出一个问题:
输入一个长度为 n 的整数序列。
接下来输入 m 个操作,每个操作包含三个整数 l,r,c,表示将序列中 [l,r] 之间的每个数加上 c。
请你输出进行完所有操作后的序列。
示例:
输入:
6 3 1 2 2 1 2 1 1 3 1 3 5 1 1 6 1输出:
3 4 5 3 4 2
这种问题看起来还是很基础的,我们可以很快的写出一般解法:
#include <bits/stdc++.h>
using namespace std;
const int N = 100010;
int a[N];
int main() {
int n,m;
scanf("%d %d",&n,&m);
for(int i = 1;i<=n;i++) scanf("%d",&a[i]);
while(m--){
int l,r,c;
scanf("%d %d %d",&l,&r,&c);
for(int i = l;i<=r;i++){
a[i] += c;
}
}
for(int i = 1;i<=n;i++) printf("%d ",a[i]);
printf("\n");
system("pause");
return 0;
}对于这个问题,如果m的数值增大、l到r的区间跨度增大,对于我们的一般写法而言,程序的执行次数则会迅速增长,时间效率就会下降,我们要做的就是尽可能的减小其运算次数,类比我们上一篇学习的前缀和,当时采用的是以空间换时间,预处理O(n)再O(1)复杂度查询,对于这个问题,我们能不能用相似的思路来解决呢?
二、一维差分与一维前缀和的联系以及代码实现
在上期的前缀和中,我们曾画出过这样的一个图:

通过原数组来构建前缀和数组,从而达到可以直接获取区间和,而我们现在要求解的问题为:将一个区间内的每个数都加一个值。可以发现要解决的问题也是区间问题,那我们能否通过一些前缀和的性质来帮助我们解决问题呢?
细心的同学会发现,如果我将a数组中任意一个位置元素的值加一个数x,那么当前位置及之后前缀和数组都的值都会比原先多x,相同的,如果我将a数组中的任意一个位置元素的值减一个数y,那么当前位置及之后的前缀和数组的的值都会比原先少y,应用这个特点,如果在上图中s数组内的第2到第4个值都加一个数x,那么先让a数组内的第2个值加x,这样前缀和数组中后续每一个数都会比之前多x,但根据要求第4个值以后将不能再多x,所以我们同样也要让a数组中第5个值减x,这样则可以达到我们想要的结果,具体可看下图:
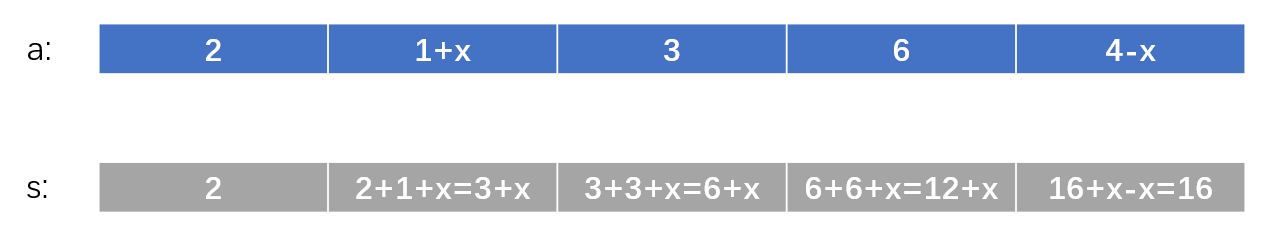
通过这样的方式我们就能将前缀和的数组中的某一区间内加或者减去一个数,也不知不觉得完成了我们之前给的需求,如果做一些总结的话我们会发现,因为前缀和数组是由原数组递推得到,则改变原数组的值即可对前缀和数组进行更改,且一次只需要改变一到两个值,就可让前缀和数组发生一段区间内值的改变,对于这个而言,前缀和数组的使用意义已经改变,他从一个“求解数组”变为了“待求解数组”,而原数组包含了一种规律,使前缀和数组可通过递推达到想呈现的状态,我们称原数组为差分数组。
接下来我们通过文章开头所给的题目来实际模拟一下,差分数组的构建以及问题的求解过程。
1.差分数组与原数组(前缀和数组)的初始化
首先,对于初始给出的数据怎么存储这是一个值得思考的问题,我们不妨想一下在这个过程中一定要遵循的原则是什么:差分数组与原数组之间必须存在合法的递推关系,换言之,原数组的每一个值必须与原数组和差分数组递推得到的值一样。原数组的初始值肯定为第一次输入的值,这个毋庸置疑,对应到上面的输入案例,原数组中存有的元素则为:

对于差分数组的处理,我们可以取一个极限,在最初始的输入过程中,原数组输入的每一个值,实际可以理解为是在[l,l]区间内加了一个数,我们刚刚处理的是从[l,r]区间内加一个相同数的解决方法,现在初始化差分数组的过程实际就为区间内加数的特殊情况,即为l = r,所以插入的方法与一般情况相同,即为:在l的位置加对应的数,在l+1的位置减去对应的数。文字说着可能不好理解,这里将初始化后的差分数组与原数组的图放在下方:

我们发现,按照这种方法差分数组与原数组递推得到的值与原数组的值是相同的,也验证了我们刚才方法的可行性,至此初始化完成。
2.通过改变差分数组的值实现原数组的区间内元素加减
这一步就很简单了,按照之前得出的规律进行差分数组中的两个元素修改(l和r+1),来构建出新的递推数组,需要m次访问则进行m次修改,修改的数组由下图所示:

3.更新原数组
在上一步的操作后,我们已经得到了满足我们所需条件的差分数组,但原数组还未得到更改,最后则需要遍历一遍原数组,通过与差分数组的递推关系而得到满足条件的新数组,这个时候方法则与求解一维前缀和的方式一样,递推公式为:
通过这一步我们就可以得到最终我们想要的数组s,至此求解完成。

4.一维差分的代码实现
讲了这么多,最后到了我们的代码实现环节,差分数组的构建和操作是具有重复性的,所以完全可以封装为一个insert函数,便于使用,接下来给出完整的实现代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 100010;
int a[N],s[N];//a数组为差分数组,s数组为原数组
void insert(int l,int r,int c){
s[l] += c;
s[r+1] -= c;
}
int main() {
int n,m;
scanf("%d %d",&n,&m);
for(int i = 1;i<=n;i++){
scanf("%d",&a[i]);
}
for(int i = 1;i<=n;i++){
insert(i,i,a[i]);//初始化差分数组
}
while(m--){
int l,r,c;
scanf("%d %d %d",&l,&r,&c);
insert(l,r,c);//更新差分数组
}
for(int i = 1;i<=n;i++){
a[i] = a[i-1] + s[i];//更新原数组
printf("%d ",a[i]);
}
return 0;
}三、二维差分的推导及代码实现
与前缀和一样,差分也有一维差分而二维差分,接下来可以给各位一个具体的题目,让大家知道二维差分的应用场景:
输入一个 n 行 m 列的整数矩阵,再输入 q 个操作,每个操作包含五个整数 x1,y1,x2,y2,c,其中 (x1,y1)和 (x2,y2) 表示一个子矩阵的左上角坐标和右下角坐标。
每个操作都要将选中的子矩阵中的每个元素的值加上 c。
请你将进行完所有操作后的矩阵输出。
示例:
输入:
3 4 3 1 2 2 1 3 2 2 1 1 1 1 1 1 1 2 2 1 1 3 2 3 2 3 1 3 4 1输出:
2 3 4 1 4 3 4 1 2 2 2 2
一维差分解决的是在一维情况下一段区间内加或减一个数,二维差分解决的则是在一个矩阵中加或减一个数,差异则是在构建差分数组时不同的构建方法,考虑到升维后每个人的理解能力会有不同,本期则用另外一种方法去推导公式,如果对上一期的方法掌握较好也完全可以自己去推导相应的公式。
1.只观察x1-x2,y1-y2,将其看成两个一维数组
我们可以先完成局部的构建,若后续出现纰漏再增加条件,这样可以有效的减少我们的思维量,对于这次来讲,我们先看化成矩阵的上边和左边,对于两条边来讲我们完全可以看成是一维数组,因为只有行或列的其中一个发生了变化,变化范围与一维情况一致,如图所示阴影部分则是这一段内需要加一个数c的区域(图中的数组为差分数组):
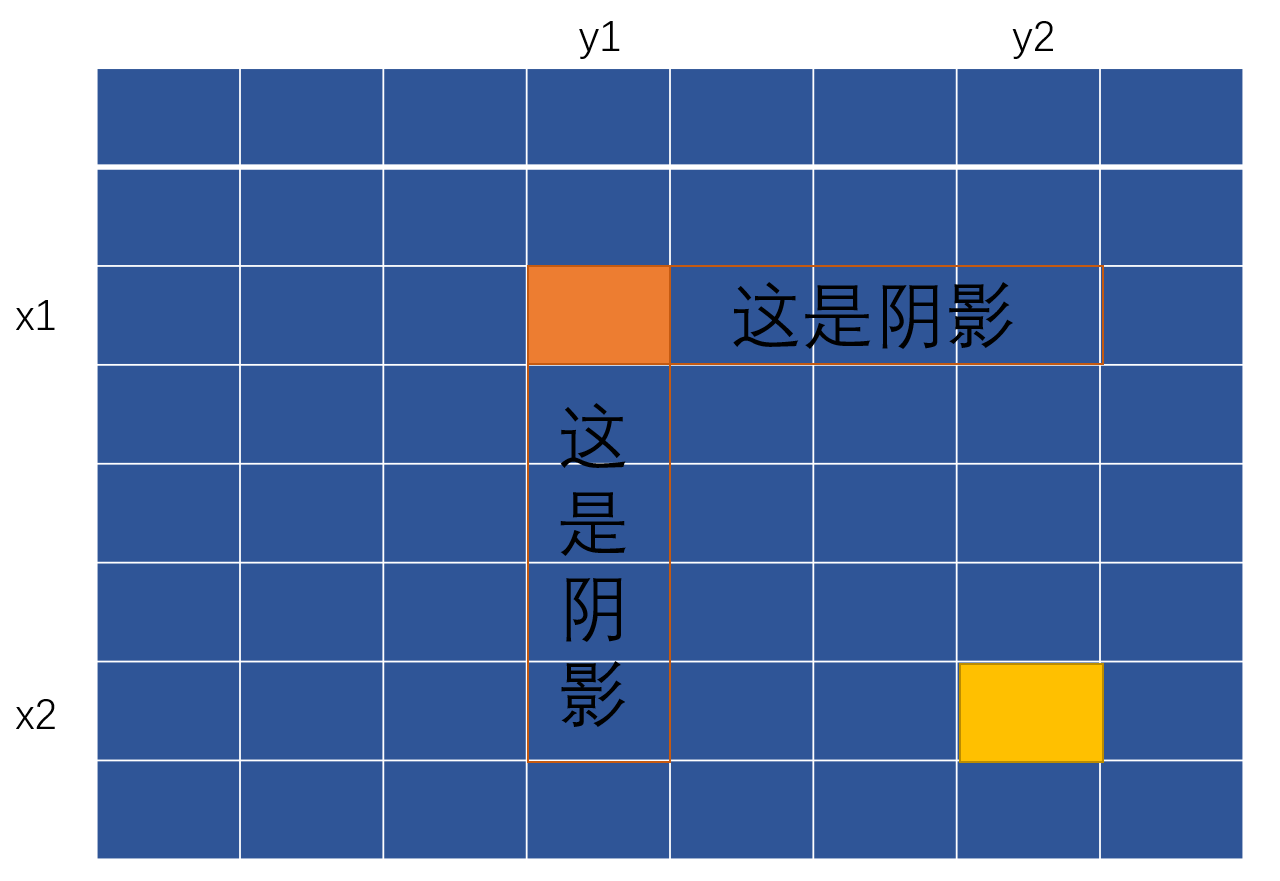
所以我们首先可以写出在差分数组中加c的的代码:
经过上述操作后,已经可以保证在这个矩阵内的所有数都加上c,但与一维情况一样,需要控制边界,让在闭区间后的所有方格不再加c,即在差分数组中对应的坐标下-c,在一维的情况下,我们要在对应的闭区间+1处减去c,我们先将两个特殊情况处理好,对应的坐标则是(x2+1,y1)与(x1,y2+1),对应到代码上则为:
2.升维扩展,找漏洞
在通过对特殊情况下的边界处理后,我们下一步做的则是扩展区间,验证特殊情况是否能满足一般情况,但要怎么验证呢?到这个节点也许我们都已经忘了一个很重要的结论——差分数组就是前缀和数组的原始数组,我们学习过二维前缀和的递推方式,所以可以通过求解每个边界格子中的前缀和来验证构建差分数组是否有漏洞。
我们将边界从(x2+1,y1)保持纵向距离不变逐渐扩展横向距离到(x2+1,y2+1)。
为什么是+1?
1.因为这一点控制的差分数组的收尾,我们需要判断的是后续的元素是否有出现多减和少减的情况出现,如果出现推出的前缀和与期望的值不同,则说明构建差分数组时对边界的处理有纰漏,若期望相同则说明边界处理无异常,结果正确。
2.执行a[x1] [y1] += c;后如果不加处理后续的所有格子都会加c,所以不需要考虑格子内的值是否异常,只需要考虑边界-c的部分。
扩展到(x2+1,y2+1)的原因是这个点为验证条件的临界点,在这个点时求解的前缀和恰好为横向处理的临界点和纵向处理的临界点,若这个点的值正常,则就完全可以得出推导正确的结论。
图中框起来的是有变化的方格,计算前缀和时是要用到从起始到该点围住的所有方格。
首先对(x2+1,y1)这一点求前缀和,显然结果正确,与一维情况一致,过。
然后将边界向右移动一次并对(x2+1,y1+1)这个点求解前缀和,如下图所示,我们会发现结果依然正常,继续向后移动。
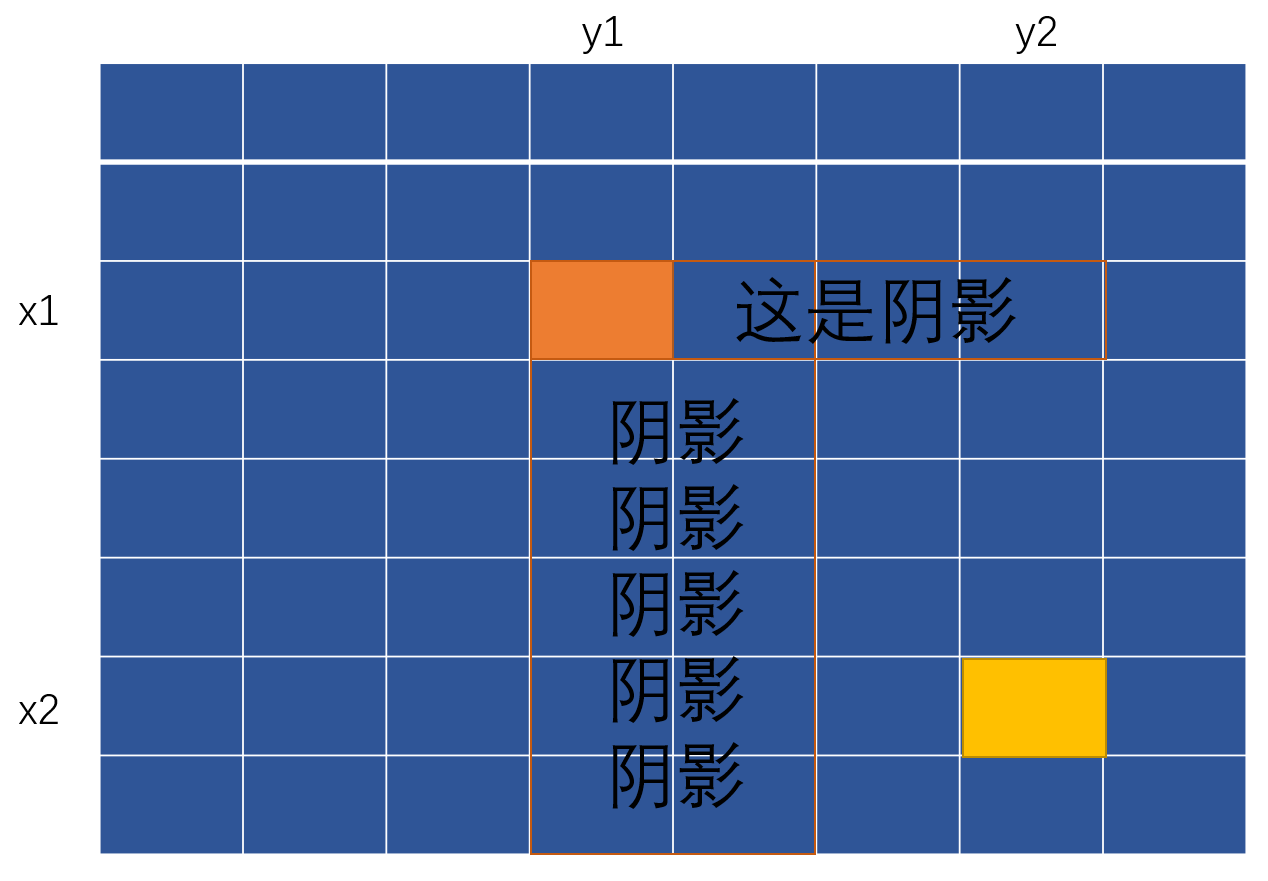
一直到最后的(x2+1,y2+1),我们会发现小小的问题,在之前的操作中为了防止区间外也加c,分别在横纵边界的后一个数设置了-c(不明白看图),这一操作在之前的滑动中都没有出现问题,但当到(x2+1,y2+1)时我们发现此时围成的区域内一共减了2c,这就导致算出的结果异常,所以在这个地方需要进行特殊操作,即:
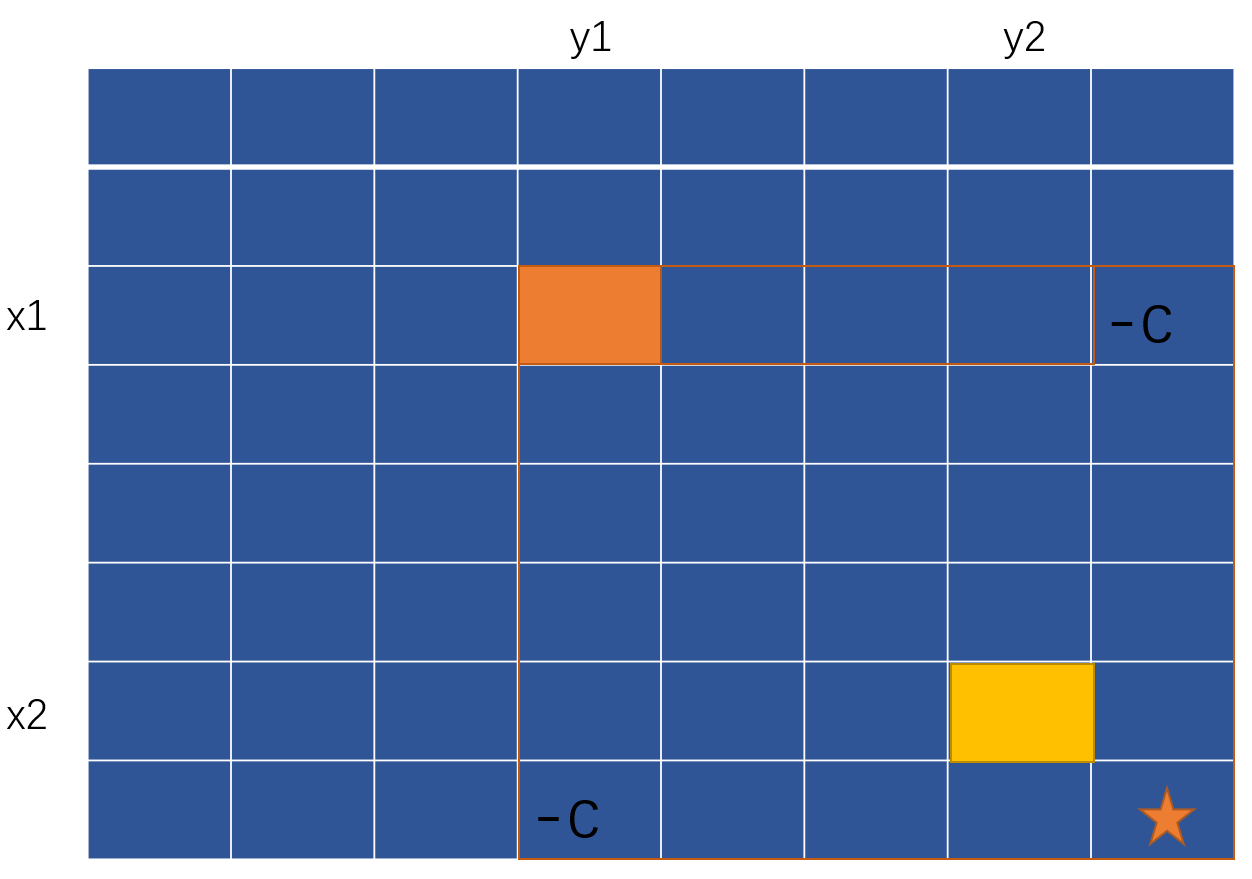
3.推广到一般,并代码实现
经过上述的艰难推导,我们终于得到了构建二维差分数组的方法,那么在初始化的阶段则与一维差分相同,可以给极限为在下标[i,i]和[j,j]中加一个数c,套用上述的推导公式。在后续更新时也只需要用构建二维前缀和数组的公式,即可得到所求数组,那么接下来将给出完整的实现代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int a[N][N],s[N][N];//a为差分数组,s为原数组(前缀和数组)
int n,m,q;
void insert(int x1,int y1,int x2,int y2,int c){
//构建二维差分数组
a[x1][y1] += c;
a[x2+1][y1] -= c;
a[x1][y2+1] -= c;
a[x2+1][y2+1] += c;
}
int main() {
scanf("%d %d %d",&n,&m,&q);
for(int i = 1;i<=n;i++){
for(int j = 1;j<=m;j++){
scanf("%d",&s[i][j]);
}
}
//构建初始差分数组
for(int i = 1;i<=n;i++){
for(int j = 1;j<=m;j++){
insert(i,j,i,j,s[i][j]);
}
}
while(q--){
int x1,y1,x2,y2,c;
scanf("%d %d %d %d %d",&x1,&y1,&x2,&y2,&c);
//更新差分数组
insert(x1,y1,x2,y2,c);
}
for(int i = 1;i<=n;i++){
for(int j = 1;j<=m;j++){
//更新原数组
s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];
}
}
for(int i = 1;i<=n;i++){
for(int j = 1;j<=m;j++){
cout << s[i][j] << " ";
}
cout << endl;
}
return 0;
}四、总结
通过今天的学习,相信对前缀和与差分的优化类思想有了更深的认识,在有些题目中巧妙应用这种优化思想可以大幅提升程序的运行效率,并且在学习中的以空间换时间这一思想也是非常重要的,能增强各位对这一类思想的认识。
好了本期内容到这里就结束了,如果你认为该文章对你有一点点帮助,也请希望收藏我的主页或者关注微信公众号:ModCx,如果有什么疑问或者建议也可在微信公众号后台留言,你们的支持就是我的动力,让我们下期再见~

Orz %%%